Hintergrundwissen: Gruppenlaufzeit, Phase und Delay

Zielgruppe

Alle, die ein gewisses technisch naturwissenschaftliches Interesse haben und das Kapitel Hintergrundwissen bereits gelesen haben. Alle, die Dinge wie "Phase", "Delay", zeitkorrigierte Lautsprecher, Laufzeitkorrekturen mit FIR-Filtern genauer verstehen möchten.

Die Gruppenlaufzeit (GLZ, Symbol $\tau_{gr}$, gemessen in Millisekunden) gibt an, wie lange es dauert, bis eine bestimmte Frequenz wiedergegeben wird, nachdem das Signal am Eingang angelegt wurde. Im allgemeinen Sprachgebrauch ist dabei oft nur das frequenzabhängige Laufzeitverhalten des Übertragungssystems gemeint. Der konstante (für alle Frequenzen gleiche) Anteil wird oft getrennt betrachtet und als Signalverzögerung (Delay) bezeichnet. Er ist z.B. wichtig um Bild und Ton zu synchronisieren, ändert den Klang aber nicht. Entscheidend für den Klang ist nur, ob verschiedene Frequenzen zeitlich auseinanderlaufen. Ein "schwerfälliger" Tieftöner ist beispielsweise durch eine längere Gruppenlaufzeit im Bassbereich zu erkennen. Bei der Wiedergabe könnte z.B. Schlagzeug dadurch "zu wenig impulsiv" wirken. Bei höheren Frequenzen wird es besonders problematisch, wenn sich das Laufzeitverhalten beider Stereo Kanäle (z.B. durch einen unsymmetrischen Hörraum) unterscheidet. Schlechte Ortbarkeit und Klangverfärbungen können die Folge sein. Entsprechende Korrekturen, z.B. durch den Einsatz von FIR-Filtern, können nach meiner Erfahrung zu beeindruckenden Verbesserungen führen.

Anfangs etwas irreführend ist die Bezeichnung "Delay" für den entsprechenden Regler am Subwoofer Ausgang. Da hier nur der Frequenzbereich des Subwoofers betroffen ist (d.h. die restlichen Lautsprecher und somit ihre Frequenzen nicht), bewirkt er eine frequenzabhängige Änderung der Gruppenlaufzeit, hat also durchaus Einfluss auf den Klang.

Grundsätzlich ist diese Zeitrichtigkeit hörbar, sonst würde ein Logsweep genauso klingen wie ein Knall. Umstritten ist a) ab wann und b) ob auch Phasendrehungen hörbar sind. Die Effekte sind vergleichsweise gering. Ohne Maßnahmen an der Raumakustik, die Optimierung der Aufstellung der Lautsprecher und/oder des/der Subwoofer(s) braucht man sich wohl nicht mit der GLZ zu beschäftigen, danach sicherlich im High End Bereich, ansonsten vielleicht. Konkrete Sachverhalte, die hoffentlich ein wenig zur Klarheit beitragen:

Ab wann sind Laufzeiteffekte hörbar?

Die Hörschwelle hängt stark von Raum, Equipment und Hörer ab. Bis heute wird häufig [Blauert 1978] als Anhaltspunkt verwendet:
"Frequency Threshold of Audibility
8 kHz 2 ms
4 kHz 1.5 ms
2 kHz 1 ms
1 kHz 2 ms
500 Hz 3.2 ms"
Bei Frequenzen im Bereich unter 100 Hz liegt die Hörschwelle bei deutlich höheren Werten, vermutlich im Bereich von 10 bis 20 ms [Neumann], ein Anstieg der Laufzeit von 10 auf 40 ms führt zu "relevanten Unterschieden" [Goertz 2001].

Die Beispielmessungen mit der App "Subwoofer Optimizer" zeigen für die elektrostatischen Lautsprecher Unregelmäßigkeiten in der Gruppenlaufzeit, die in dieser Größenordnung liegen. Die preiswerteren dynamischen Lautsprecher in einem weniger gedämmten Hörraum haben deutlich schlechtere Werte. Diese Unterschiede sind deutlich hörbar. Die preiswerteren Lautsprecher liefern im besser gedämmten Wiedergaberaum zwar mehr Klangdefinition durch den reduzierte Diffusschall, die Akzentuiertheit der Elektrostaten kann aber nicht erreicht werden.

Der subjektive Unterschied hängt nach eigenen Versuchen vom Tonmaterial (impulsartig, periodisch) ab. Auch ungeübte Hörer hören die Unterschiede mühelos, soweit sie die innere Ruhe haben, sich auf das Hörerlebnis einzulassen. Korrekturen der GLZ durch FIR-Filter verbessern die Situation erheblich, schließen die Lücke zwischen den verschiedenen Lautsprechern aber nicht.

Laut Literatur spielen zusätzlich die Abhörlautstärke und psychoakustische Diskrepanzen (kleine Räume, die wie große Konzertsäle klingen sollen) eine Rolle. Die Mikrofonierung beeinflusst das Ergebnis vermutlich auch: durch den Einsatz vieler Mikrofone pro Instrument könnte die Zeitrichtigkeit beeinflusst werden, da ein Instrument verschiedene Teile des Klangspektrums in verschiedene Richtungen abstrahlt. Dadurch könnte ein weiter entferntes Mikrofon beispielsweise mehr tiefe Frequenzen und ein näheres Mikrofon (etwas früher) mehr hohe Frequenzen auffangen.

Der Autor dieser Zeilen wohnt in der Nähe der Jesus-Christus-Kirche in Berlin Dahlem, die international für ihre hervorragende Akustik bekannt ist - trotz "lausiger" Nachhallzeiten gemessen an den Vorgaben von DIN 18041 [Burkowitz, Fuchs 2009], und damit sicherlich auch entsprechender GLZ. Er war bei zahlreichen Tonaufnahmen dort anwesend und kann die Klangqualität bestätigen.

Ist nur ein kleiner Frequenzbereich verzögert, ist das weniger hörbar. In [Goossens] wird das mit künstlich verzerrtem Händeklatschen untersucht. Offenbar liegt das daran, dass dann auch nur wenig Energie verspätet abgegeben wird: Erst wenn durch veränderte Gruppenlaufzeiten ein deutlicher zweiter Impuls (größer als die Nachhörschwelle) in den Energiekurven sichtbar wird, beginnt die Hörbarkeit.

Um die Effekte durch die Gruppenlaufzeit (nur diese sind mit dem Delay-Regler korrigierbar) von all diesen Seiteneffekten zu trennen, bieten sich folgende Möglichkeiten:

Statements zur GLZ

Einerseits gehört die GLZ in das Aufgabenfeld von Komponentenherstellern und Toningenieuren mit entsprechendem Wissen und jahrelanger Erfahrung, andererseits bieten heute manche Komponenten Einstellmöglichkeiten an (Filtercharakterisk wie Bessel, Tschebyscheff, Butterworth oder auch Linearphasigkeit bzw. Minimalphasigkeit bei FIR-Filtern), die im Grunde solches Wissen voraussetzen. Ob ein theoretischer Backgruond letztlich zu besseren Resultaten führt, oder ob die aufgewendete Zeit (wegen vieler Seiteneffekte) doch besser in Versuch und Irrtum investiert ist, ist eine vielschichtige Frage, deren Diskussion i.d.R. ergebnislos endet.

Messung der GLZ

Room Acoustics Meter und andere Apps aus der Hifi-Apps Serie bieten die Möglichkeit, die GLZ zu messen. Die Ergebnisse hängen dabei sehr stark von Einstellungen und Methode ab, d.h. eine ohne Vorkenntnisse durchgeführte Messung wird bestenfalls zufällig brauchbare Ergebnisse liefern. Der "Messaufbau" hier sind zwei MartinLogan Masterpiece Classic ESL 9. Der Dipol-Charakter zusammen mit dem schnellen Ansprechverhalten dieser Elektrostaten (bzw. das auch nach hinten abstrahlende Tieftönerpaar im Sockel) liefert gute Voraussetzungen, um die Eigenheiten solcher Messungen zu demonstrieren: Einerseits ist an den Aufstellungsorten der Lautsprecher eine erhebliche Schallschnelle zu erwarten, die zu entsprechend ausgeprägten Druckänderungen an den Wänden führt. Der Raum wird also "kräftig mitspielen". Andererseits wirken die Lautsprecher im Klang trotzdem präzise. Im rot dargestellten Frequenzgang des rechten Kanals "Frequency Response (Raw)" ist eine entsprechend deutliche Resonanz bei 80 Hz sichtbar, zu 90 Hz hin fällt er stark ab:

Mit der starken Amplitudenänderung ist eine entsprechend starke Phasendrehung verbunden, sodass die GLZ "Group Delay (Raw)" buchstäblich um mehr 500 ms springt. Das ist zugegebenermaßen eine Art Rekord-Wert, aber Änderungen über 100 ms bei kaum 10% Frequenzänderung sind keine Seltenheit, unabhängig von Hörraum, Equipment und Software. Schon das ist natürlich kontraintuitiv - sicherlich gibt es kein Wohnzimmer in dem zwei so benachbarte Töne derart unterschiedlich ankommen, als hätten sie einen Wegunterschied von ca. 30 m (100 ms) durchlaufen, und über 150 m (500 ms) schon gar nicht. 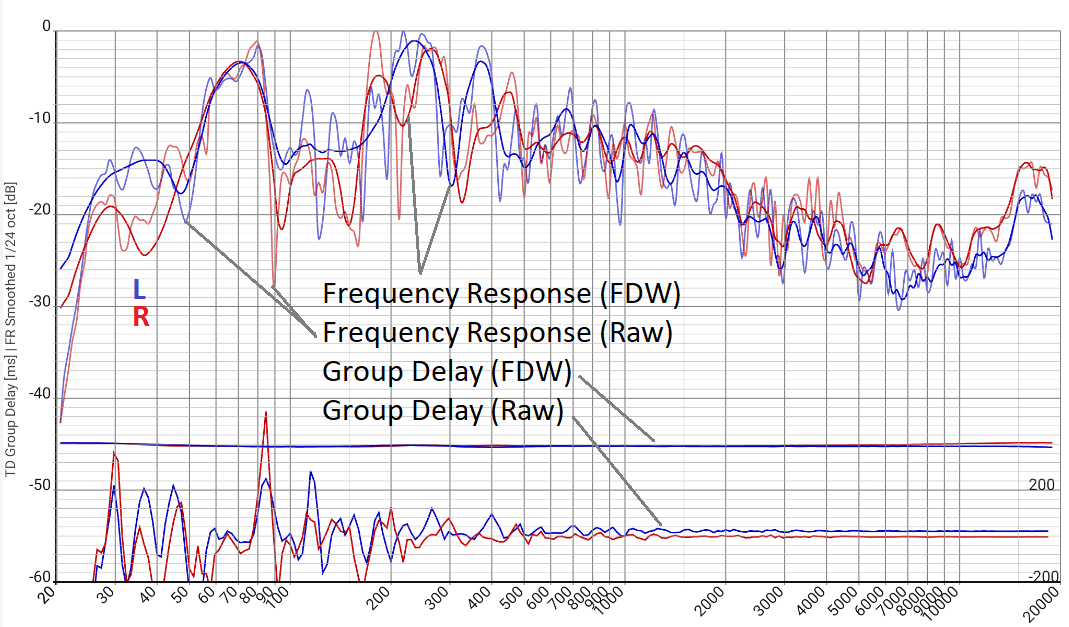Die Kurve "Group Delay (FDW)" zeigt die selben Messdaten im selben Maßstab, aber mit frequenzabhängiger Fensterung FDW (siehe später). Der Wertebereich von vielleicht 20 ms ist gerade noch erkennbar und sicherlich viel sinnvoller.

Als Autor von App und Dokumentation wollte ich der Sache sicherheitshalber weiter auf den Grund zu gehen. Einige der Ergebnisse sind so interessant, dass ich sie hier zeigen möchte. Zur Untersuchung habe ich Bursts mit diesen Frequenzen abgespielt und die Oszillogramme mit denen der Mikrofonsignale verglichen. Weil manche Singularitäten bei Wellen im Zusammenhang mit Nichtlinearitäten stehen, habe ich das wirkliche physikalische Mikrofonsignal statt einer berechneten Faltung dieser Bursts mit der Impulsantwort angesehen.


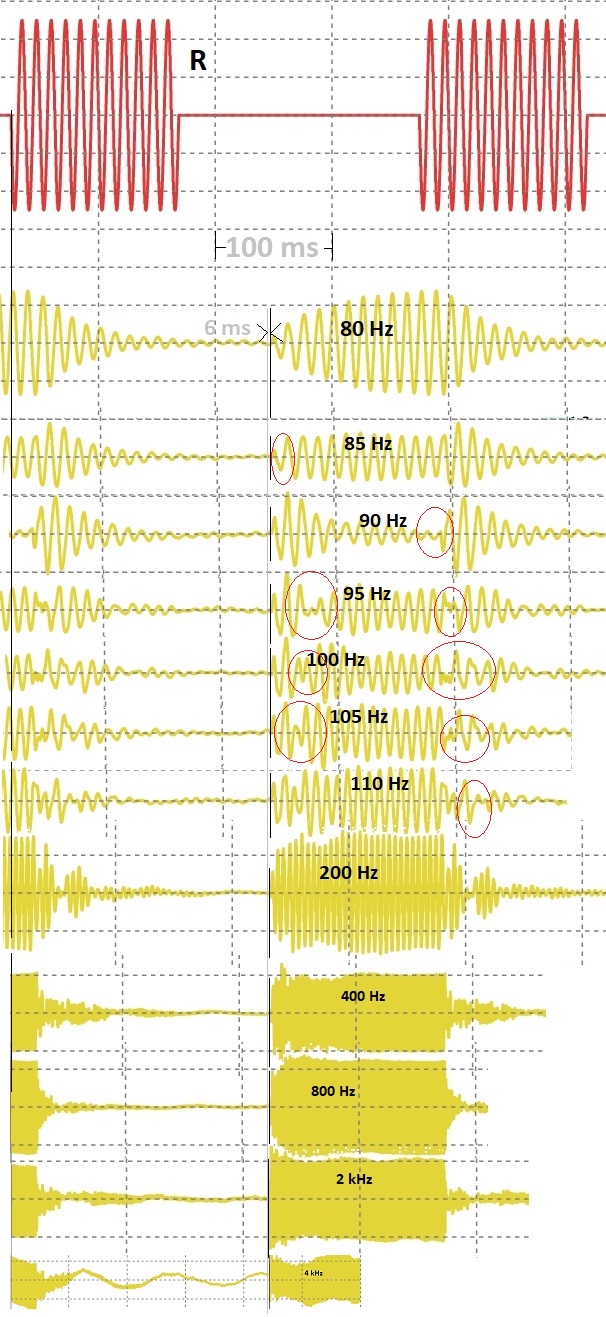
Bursts, abgespielt und aufgenommen mit Hifi-Apps Car Audio Setup. Rot: Abgespielter Burst (nur für 80 Hz gezeigt). Gelb: Mikrofonsignale aller Frequenzen. Die Anfänge wurden in immer gleichen Abständen zu den jeweiligen abgespielten Signalen ausgerichtet (daher die Sprünge im Gitter) und mit einer dünnen schwarzen Linie markiert. Die senkrechte graue Linie 6 ms davor dient nur zur Orientierung.

Man erkennt auf den ersten Blick, dass sich die Anfänge der Bursts höchstens um wenige ms verschieben, Verschiebungen in der oben genannten Größenordnung sind wie zu erwarten undenkbar. Die Herkunft dieses Effektes ist aber trotzdem zu sehen: An den rot eingekreisten Stellen springt die Phase. Es liegt nahe, dass die Ursache ähnlich wie bei der Exzessphase (s.o.) im additive Zusammenspiel der Transferfunktionen des Raums zu suchen ist. Die gesamte Phase wird aber nach der Phase aller (irgendwann) ankommenden Signal-Anteile der jeweiligen Frequenz berechnet. Die GLZ berechnet sich wiederum aus der Änderung dieser gesamten Phase pro Frequenzänderung. Entsprechend erscheint im Ergebnis ein erheblicher Sprung. Technisch gesehen ist die Frequenz der Einhüllenden so nah an der Trägerfrequenz, dass nicht mehr die "Laufzeit" des Wellenpaketes beschrieben wird (siehe später).

Für den Hörsinn spielt dieser Effekt aber eine vollkommen andere Rolle als die erste Ankunftszeit des ersten Direktschalls (dünne schwarze Linien): Letztere ist für eine laufzeitbasierte Ortung der Schallquelle entscheidend. Und vermutlich sind wir die Nachfahren derer, die die laufzeitbasierte Ortung eines brüllenden Tigers unabhängig von irgendwelchen Reflexionen und Phasendrehungen, sicher beherrschten. Das kann und sollte bei der Berechnung berücksichtigt werden, indem anschaulich gesprochen (wenn schon nicht die schwarze Linie, dann wenigstens) nur die ersten Wellenzüge der Messung angesehen werden. Das wiederum ist die Hauptidee hinter FDW.

Man sieht aber auch, dass das Messergebnis ohne FDW nicht wertlos ist. Der Peak zeigt eine eindeutige Besonderheit in der Akustik an, wenn auch durch möglicherweise bereichernden indirekten Schall. Man könnte jetzt Töne mit dieser Frequenz abspielen, im Raum umherlaufen und prüfen, ob diese Besonderheit schon früher als störend wahrgenommen wurde und ggf. die Situation verbessern. Ein quantitativ sinnvolles Ergebnis erhält man erst nach FDW. Dies wird beispielsweise auch als Grundlage zur digitalen Raumkorrektur verwendet. Gängige Meinung [Barnett 2017] ist, dass digitale Raumkorrektur (DRC) auf Messungen mit FDW aufbauen muss. Für einfache Einstell-Arbeiten wie den Delay eines Subwoofers ist die geglättete Version ohne FDW dagegen vollkommen ausreichend.

Details und mögliche Kritikpunkte

Kritik: Die Auswertung erfolgte grafisch anhand der gemessenen Oszillogramme, und die Anfangszeiten wurden subjektiv an die erste sichtbare Schwingung gezeichnet. In der Rechnung weiter unten ergibt sich dagegen beispielsweise nicht dieser Anfang, sondern der Punkt des halben Anstiegs als GLZ.
Meine Antwort: Das mag in der Signaltheorie gängig sein, trägt dem logarithmischen Empfinden des Hörsinns und der Wichtigkeit des ersten Direktschalls aber nicht Rechnung. Die These "die Wahrnehmung beginnt, sobald man auf dem Oszillogramm etwas sieht" ist sicher nicht perfekt, aber näher an der Realität. Im übrigen würden sich die Werte praktisch nur bis zur 85 Hz-Messung signifikant ändern, bei den benachbarten Punkten bis 110 Hz fast nicht.

Kritik: Die Messung sollte durch die mathematisch korrekte Variante "Faltung der Impulsantwort mit den Bursts" ersetzt werden.
Meine Antwort: Das habe ich getan, es gibt keine sichtbaren Unterschiede. Die Berechnung des etwas merkwürdig anmutenden 90 Hz Oszillogramms im Vergleich zur Messung oben:

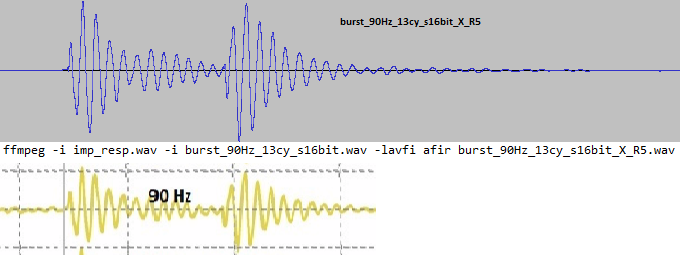
Die Effekte treten also auch in linearen, zeitinvarianten Systemen auf bzw. die Ursache ist nicht in Nichtlinearitäten zu suchen. Auch mehr Messpunkte würden keine neue Erkenntnis liefern. Im Grunde würden schon zwei Punkte reichen, um die Diskrepanz der Werte aufzuzeigen.

Kritik: Die Bursts sind nicht gefenstert, die Messung entsprechend ungenau.
Meine Antwort: Sicher erheblich genauer als die gefundenen 500 ms. Raum und Lautsprecher sorgen ohnehin für eine gewisse Fensterung und die Wellenzüge mit den zu untersuchenden Frequenzen sind in den Oszillogrammen deutlich sichtbar, gar zu stark kann der Einfluss durch die Harmonischen des umschreibenden Rechtecks mithin nicht sein.

Detail: FDW Einstellungen für den relevanten Frequenzbereich: 34-59 Hz: 132 ms Fensterbreite (je 25 ms rise / fall), 59-103 Hz: 96 ms (21 ms), 103-179 Hz: 72 ms (18 ms), also an der unteren Grenze des Gängigen (sehr kurze Fenster).

Frage: Welche Genauigkeit ist nun bei einer GLZ Messung zu erwarten?
Meine Antwort: Mit vernünftig gewählten FDW Parametern wohl hoffentlich im Bereich der Wahrnemungsschwelle des Hörsinns, aber auch nicht viel besser. Im Grunde müsste man sich die Oszillogramme verschiedener Frequenzen einzeln (automatisiert?) ansehen und mit dem Wissen über Psychoakustik abgleichen. Berechnet man aus des gemessenen Phase eine DRC, sollte man ganz einfach verschiedene Auswertungen durchführen und per Hörtest das beste Ergebnis suchen.

Phase

Man kann die Phase eines Subwoofers um 180° drehen, indem man den Lautsprecher umpolt. Insbesondere bei Subwoofern, die auf der zu den Lautsprechern gegenüberliegenden Seite platziert sind, kann das den Klang verbessern. Einige Soundprozessoren bieten auch feinere Phaseneinstellungen zwischen 0 und 180° an, das kann den Klang weiter verbessern.

Videos

Teil 1 von 4: Wofür ist der Phasenregler beim Subwoofer, was bedeutet Delay? Wie kann man das mit Zentimetermaß und Smartphone einstellen?

Teil 2 von 4: Was macht die Speaker Management Unit Behringer Ultra Drive DCX 2496 genau, wenn man Phase und Delay einstellt? Funktionsgenerator und Oszilloskop zeigen Details, die mit Soundkarte und Software nicht zu sehen sind. Nebenbei wird durch Zufall eine interessante Eigenheit des 2 kW Class D Verstärker STA 2000D von IMG Stageline gefunden.

Teil 3 von 4: Was messen und zeigen Softwareprodukte wie REW oder Acourate?

4. Phase und Delay: Interpretation der Ergebnisse

Verbesserungsmöglichkeiten

Neben den oben beschriebenen Verbesserungsmöglichkeiten geben Hifi-Apps anhand der Impulsantworten der einzelnen Lautsprecher an den einzelnen Hörplätzen weitere Hinweise. Das Thema wird ständig weiter entwickelt, so dass hier nur einige allgemeine Statements erfolgen: Insbesondere eindeutige Schwächen in der Kanalgleichheit und auch Nachhallzeiten, die auf sehr wenig Dämpfung hinweisen können den Klang deutlich verschlechtern. Beides lässt sich mit Hifi-Apps leicht messen und oft genauso einfach korrigieren. Vor jeder Messung sollten die allgemeinen Hinweise zur Aufstellung von Lautsprechern und zur Aufstellung von Subwoofern berücksichtigt werden.

Für Techniker

Durch die Fouriertransformation der Transferfunktion eines linearen zeitinvarianten Systems wird eine Zeitverschiebung (Delay) $\tau_{d}$ zu einer frequenzproportionalen Phasendrehung: $ \mathscr{F}\{ F(\omega)\} = f(t) \Rightarrow \mathscr{F}\{\exp(i \omega \tau_{d}) F(\omega)\} =f(t-\tau_{d})$ wobei $\omega$ die Kreisfrequenz und $t$ die Zeit ist. Anders ausgedrückt kann in diesem einfachen Fall die Transferfunktion als $H(\omega)=k\exp(i \omega \tau_{d}) $ angesetzt werden, also $$ \begin{align} |H( \omega)| &= k \\ \angle H( \omega) &: = \varphi = -\omega \; \tau_{d}\\ \end{align} $$ Wegen des linearen Zusammenhangs zwischen $\omega$ und $\angle H(\omega)$ kann der Delay folglich sowohl als Bruch als auch als Differenzialquotient geschrieben werden: $$ \tau_{d} = - \frac{ \varphi( \omega)}{\omega} = - \frac{ \mathrm{d}\varphi( \omega)}{\mathrm{d}\omega} $$

Alternativ kann man von einem frequenzabhängigen Verhalten der Transferfunktion ausgehen. Vernachlässigt man den für das Zeitverhalten unwichtigen Betrag $\frac{\mathrm{d}}{\mathrm{d\omega}} |H(\omega)| = 0$, so beschreibt $\tau_{d}=-\varphi'$ das erste Glied der Taylor-Entwicklung von $H$ um $\omega_0$: $$ \begin{align} Y_k(\omega) &= H_k(\omega) X_k(\omega) \\ &= |H(\omega_0)| \exp\Big(i \varphi(\omega_0) + i (\omega-\omega_0) \varphi'(\omega_0) \Big) X_k(\omega) \\ &= \Bigg( |H(\omega_0)| \exp\Big(i \varphi(\omega_0) -i \omega_0 \varphi'(\omega_0) \Big) \Bigg) \exp\Big(i \varphi'(\omega_0)\omega\Big) X_k(\omega) \end{align} $$ Die erste Klammer hat einen konstanten Wert, die zweite Klammer charakterisiert die Phasendrehung durch den Delay.
Anschaulich besagen beide Gleichungen, dass wenn zur Überbrückung einer bestimmten Entfernung ein Wellenzug einer bestimmten Frequenz benötigt wird, o.B.d.A. zwei Wellenzüge der doppelten Frequenz benötigt werden. In der realen Welt geht dieser einfache Zusammenhang natürlich verloren. Es bleibt aber sinnvoll, die Phasendrehung in einen trivialen Anteil $\tau_{pd}$ zur Beschreibung der Zeitverschiebung und den (meist entscheidenden) Anteil, der die Frequenzabhängigkeit des Systems durch Resonanzen, Filtereffekte usw. bestimmt zu splitten. $$ \begin{align} \tau_{pd} &= -\frac{\mathrm{d} \varphi(\omega)}{\mathrm{d}\omega} \bigg \vert_{\omega = \omega_0} \\ \tau_{gr} &= -\frac{\mathrm{d} \varphi(\omega)}{\mathrm{d}\omega} \\ \end{align} $$ Software zur Darstellung der Gruppenlaufzeit bietet deshalb eine "Unroll-Funktion" an, die automatisch oder manuell den Abzug eines $\tau_{pd}$-Anteils ermöglicht. Damit erhält der User die Möglichkeit, das durch Resonanzen, Filtereffekte usw. bestimme Systemverhalten ohne störende Phasendrehungen anzusehen. In der Praxis spielt dieser Anteil in sehr viel langsameren Zeitskalen als die Periodendauer des Signals, er verändert eher die Einhüllende. Wie oben gezeigt muss das bei Messungen der Raumakustik durch entsprechende Fensterung sichergestellt werden, andernfalls spiegelt $\tau_{gr}$ nichts die gängige Definition "...wie lange es dauert bis eine bestimmte Frequenz wiedergegeben wird.." wider. Setzt man man ein Signal mit einer Trägerfrequenz $\omega$ an, das durch eine Einhüllende moduliert wird, dann teilen sich $\tau_{gr}$ und $\tau_{pd}$ bei der Übertragung entsprechend auf: $$ x(t) = \underbrace{ m(t)}_{\text{ Einhüllende }} \underbrace{ \cos(\omega t)}_{\text{ Trägerfrequenz }} \longrightarrow \underbrace{ m(t-\tau_{gr} )}_{\text{ Einhüllende }} \; \underbrace{ \cos(\omega (t- \tau_{pd} ))}_{\text{ Trägerfrequenz }} $$ Ein reiner Phasen Delay $\tau_{pd}$ kann wie oben beschrieben im cos-Term untergebracht werden, der entscheidende Rest verschiebt die Einhüllende in Abhängigkeit davon, welche Frequenz sie einhüllt. Die frequenzabhängige Änderung der Amplitude wurde zur Vereinfachung weggelassen.

In zeitdiskreten Übertragungssystemen, wie sie die digitale Signalverarbeitung darstellt, wird die diskrete Gruppenlaufzeit auf das Abtastintervall $T$ bezogen: $$ \frac{\tau_d(\Omega)}{T} = - \frac{\mathrm{d}\,\operatorname{arg}\{H(e^{i\Omega})\} }{\mathrm{d}\Omega} $$ mit der auf die Abtastfrequenz $f_s$ normierten Kreisfrequenz $\Omega$: $$ \Omega = \frac{\omega}{f_\mathrm{s}} = \omega \cdot T $$ Der Vorteil der normierten Form in zeitdiskreten Systemen ist die Unabhängigkeit von konkreten Abtastfrequenzen.

Beispiel

Die Übertragungsfunktion eines diskreten Systems sei eine Mittelung über die ersten 5 Indizes, also $$ \begin{align} h[n] &= \frac{1}{5} (\delta(n) + \delta(n-1) + \delta(n-2) + \delta(n-3) + \delta(n-4)) \\ H(\Omega) &= \frac{1}{5} (e^{-i0} + e^{-i\Omega} + e^{-i2\Omega} + e^{-i3\Omega} + e^{-i4\Omega} ) \\ &= \frac{1}{5} ( e^{i2\Omega} + e^{i\Omega} + e^{0} + e^{-i\Omega} + e^{-i2\Omega} ) e^{-i2\Omega} \\ &= \frac{1}{5} ( 2 \cos(2 \Omega) + 2 \cos( \Omega) +1) e^{-i2\Omega} \\ \end{align} $$ Die cos-Terme in der Klammer (der Amplitudengang) sind reell, nur der letzte Multiplikant hat Einfluss auf die Phase. Mithin wird die Gruppenlaufzeit $$ \tau_{\rm gr}(\Omega) = - \frac{\mathrm{d}\varphi(\Omega)}{\mathrm{d}\Omega} = - \frac{\mathrm{d} (-2\Omega)}{\mathrm{d}\Omega} = 2 $$ Anschaulich ist das nachvollziehbar, wenn man sich als Signal eine Sprungfunktion vorstellt, die bei $t=t_0=0$ von 0 auf 1 springt. Erreicht das Signal das System, so wird bei $t<0$ der Output zu 0, dann bei $t=0, 1, 2, 3, 4$ zu $1/5$, $2/5$, $3/5$, $4/5$, $1$, d.h. nach der Gruppenlaufzeit ist das Mittel der Flanke erreicht.

Nebenbei bemerkt handelt es sich bei dem Beispiel um einen linearphasigen Filter: Die Phase beinhaltet nur den $\arg \exp(-i2\Omega)$ Term. Grob gesprochen kommt das letztlich durch den symmetrischen Aufbau der 5 Koeffizienten. Während linearphasige Filter durch diesen symmetrischen Aufbau i.A. ihr Maximum in der Mitte der Impulsantwort haben, hat die minimalphasige Version des selben Filters (mit gleichem Amplitudengang) die grössten Koeffizienten am Beginn ihrer Impulsantwort. Auf [falstad.com] können verschiedene Filter simuliert werden.

Manche Messgeräte können aus zwei Phasenmessungen bei benachbarten Frequenzen (Näherungswerte für) die Gruppenlaufzeit (direkt) berechnen. Die App "Subwoofer Optimizer" bestimmt die Transfer Funktion per Logsweep, der mit dem Algorithmus von Farina ausgewertet wird. Die Gruppenlaufzeit wird (nach Glättung) aus dem Differenzialquotient der Phase bestimmt.

Literatur

[Barnett] Mitch Barnett: Accurate Sound Reproduction Using DSP. ‎ Independently published (2 April 2017) ISBN-10 ‏ : ‎ 1520977905 ISBN-13 ‏ : ‎ 978-1520977904

[Blauert 1978] Blauert, J. and Laws, P: "Group Delay Distortions in Electroacoustical Systems" Journal of the Acoustical Society of America Volume 63, Number 5, pp. 1478-1483 (May 1978)

[Burkowitz, Fuchs 2009] Peter K. Burkowitz, Helmut V. Fuchs "Das vernachlässigte Bass-Fundament" Vereinszeitschrift des Verbands Deutscher Tonmeister 2/2009 p. 35

[Goertz 2001] Goertz A, Wolff M (2001) "Neue Methoden zur Anpassung von Studiomonitoren an die Raumakustik mit Hilfe digitaler Filterkonzepte" Teil 1 von 2. Fortschritte der Akustik, DAGA 2002 http://www.ifaa-akustik.de/files/DAGA2002-Teil1.PDF http://www.ifaa-akustik.de/files/DAGA2002-Teil2.PDF

[Goossens] Sebastian Goossens "Wahrnehmbarkeit von Phasenverzerrungen" Institut für Rundfunktechnik, München https://forum2.magnetofon.de/bildupload/goosphase.pdf

[MSO] Multi Subwoofer Optimizer, Andy C https://www.avsforum.com/threads/optimizing-subwoofers-and-integration-with-mains-multi-sub-optimizer.2103074/

[Münker 2016] Christian Münker: "DSP auf FPGAs: Kap. 5-2 Do-It-Yourself FIR Filterentwurf" https://www.youtube.com/watch?v=y0PNXUI5x1U

[falstad.com] "...some educational applets I wrote to help visualize various concepts in math, physics, and engineering..."
http://www.falstad.com/mathphysics.html
http://falstad.com/dfilter/

[Welti Devantier] Todd Welti, Allan Devantier: Low-Frequency Optimization Using Multi Subwoofers. Harman International Industries Inc. Northbridge CA 91329 USA, Manuscript received 2006

[earl Geddes] mehlau.net/audio/multisub_geddes

[Welti Harman] Subwoofers: Optimum Number and Locationsby Todd Welti Research Acoustician, Harman International Industries, Inc.twelti@harman.com multsubs_0.pdf links folien rechts text Seite 4 "Multiple Subwoofers != Multiple Subwoofer Channels"

[Earl Geddes - YoutTube] Earl Geddes on Multiple Subwoofers in Small Rooms https://www.youtube.com/watch?v=SCWL-zusyqw

[MSO Software] https://www.andyc.diy-audio-engineering.org/mso/html/rev_hist.html

Forendiskussion. Aktuell (Okt 2020) 234 Seiten. https://www.diyaudio.com/forums/subwoofers/134568-multiple-subs-geddes-approach-149.html

Eine Art Review mit Raummoden, Welti, Geddes etc. Subwoofer / Low Frequency Optimization By Amir Majidimehr [Note: This article was published in the May/June 2012 issue of Widescreen Review Magazine]