Background knowledge: Group delay, Phase und Delay

Target audience

All who have some technical scientific interest and have read the chapter Background knowledge. Anyone who wants to understand things like "phase", "delay", time-corrected speakers, delay corrections with FIR filters in more detail.

The group delay (GD, symbol $\tau_{gr}$, measured in milliseconds) indicates how long it takes for a certain frequency to be reproduced after the signal has been applied to the input. In common usage, this often refers only to the frequency-dependent delay behavior of the transmission system. The constant component (the same for all frequencies) is often considered separately and referred to as signal delay. It is important, for example, to synchronize image and sound, but does not change the sound. The only decisive factor for the sound is whether different frequencies diverge in time. A "sluggish" woofer can be recognized, for example, by a longer group delay in the bass range. During playback, drums, for example, could appear "too little impulsive" as a result. At higher frequencies it becomes especially problematic if the delay time behavior of both stereo channels differs (e.g. due to an unbalanced listening room). Poor localization and sound coloration can be the result. Appropriate corrections, e.g. by using FIR filters, can lead to impressive improvements in my experience.

Initially somewhat misleading is the designation "Delay" for the corresponding control at the subwoofer output. Since only the frequency range of the subwoofer is affected here (i.e. the remaining speakers and thus their frequencies are not), it causes a frequency-dependent change of the group delay, so it definitely has an influence on the sound.

In principle, this time correctness is audible, otherwise a log sweep would sound just like a bang. What is disputed is a) from when and b) whether phase rotations are also audible. The effects are comparatively small. Without measures on the room acoustics, the optimization of the placement of the speakers and/or of the subwoofer(s) you probably do not need to deal with the GD, after that certainly in the high end area, otherwise maybe. Concrete facts that hopefully contribute a little to clarity:

At what point are runtime effects audible?

The threshold of hearing depends strongly on room, equipment and listener. Until today, [Blauert 1978] is often used as a reference:
"Frequency Threshold of Audibility
8 kHz 2 ms
4 kHz 1.5 ms
2 kHz 1 ms
1 kHz 2 ms
500 Hz 3.2 ms"
For frequencies in the range below 100 Hz, the hearing threshold is at much higher values, probably in the range of 10 to 20 ms [Neumann], an increase of the transit time from 10 to 40 ms leads to "relevant differences" [Goertz 2001].

The example measurements with the app "Subwoofer Optimizer" show irregularities in the group delay for the electrostatic speakers that are in this order of magnitude. The lower-cost dynamic speakers in a less damped listening room have significantly worse values. These differences are clearly audible. The less expensive loudspeakers provide more sound definition in a better damped reproduction room due to the reduced diffuse sound, but the accentuation of the electrostats cannot be achieved.

According to own experiments, the subjective difference depends on the sound material (impulsive, periodic). Even untrained listeners hear the differences effortlessly, as far as they have the inner peace to engage in the listening experience. Corrections of the GD by FIR filters improve the situation considerably, but do not close the gap between the different speakers.

According to the literature, monitoring volume and psychoacoustic discrepancies (small rooms that are supposed to sound like large concert halls) also play a role. The miking probably also influences the result: by having many microphones per instrument, time correctness could be affected, as one instrument radiates different parts of the sound spectrum in different directions. This would allow a microphone further away to pick up more low frequencies, for example, and a closer microphone (slightly earlier) to pick up more high frequencies.

The author of these lines lives near the Jesus-Christus-Kirche in Berlin Dahlem, which is internationally known for its excellent acoustics - despite "lousy" reverberation times measured against the specifications of DIN 18041 [Burkowitz, Fuchs 2009], and thus certainly corresponding GD. He was present at numerous sound recordings there and can confirm the sound quality.

If only a small frequency range is delayed, GD is less audible. In [Goossens] this is investigated with artificially distorted hand claps. Obviously, this is due to the fact that then also only little energy is delivered late: Only when a clear second impulse (larger than the post-listening threshold) becomes visible in the energy curves due to changed group travel times does audibility begin.

To separate the effects from all these side effects by the group delay (only these can be corrected with the delay control), the following options are available:

Statements about the GD

On the one hand the GD belongs to the field of activity of component manufacturers and sound engineers with appropriate knowledge and years of experience, on the other hand today some components offer adjustment possibilities (filter characteristics like Bessel, Chebyshev, Butterworth or also linear phasing or minimum phasing with FIR filters), which basically require such knowledge. Whether a theoretical backgruond ultimately leads to better results, or whether the time spent (because of many side effects) is better invested in trial and error, is a complex question whose discussion usually ends without results.

Measurement of GD

Room Acoustics Meter and other apps from the Hifi Apps series offer the option of measuring the GD. The results depend very much on the settings and method, i.e. a measurement carried out without prior knowledge will at best provide useful results by chance. The "measurement setup" here is two MartinLogan Masterpiece Classic ESL 9. The dipole character together with the fast response of these electrostats (and the pair of woofers in the base that also radiate to the rear) provide good conditions for demonstrating the peculiarities of such measurements: On the one hand, a considerable velocity of air particles is to be expected at the locations where the speakers are installed, which leads to correspondingly pronounced pressure changes on the walls. The room will therefore "play along strongly". On the other hand, the speakers still produce a precise sound. In the frequency response of the right channel "Frequency Response (Raw)" shown in red, a correspondingly clear resonance is visible at 80 Hz, dropping sharply towards 90 Hz: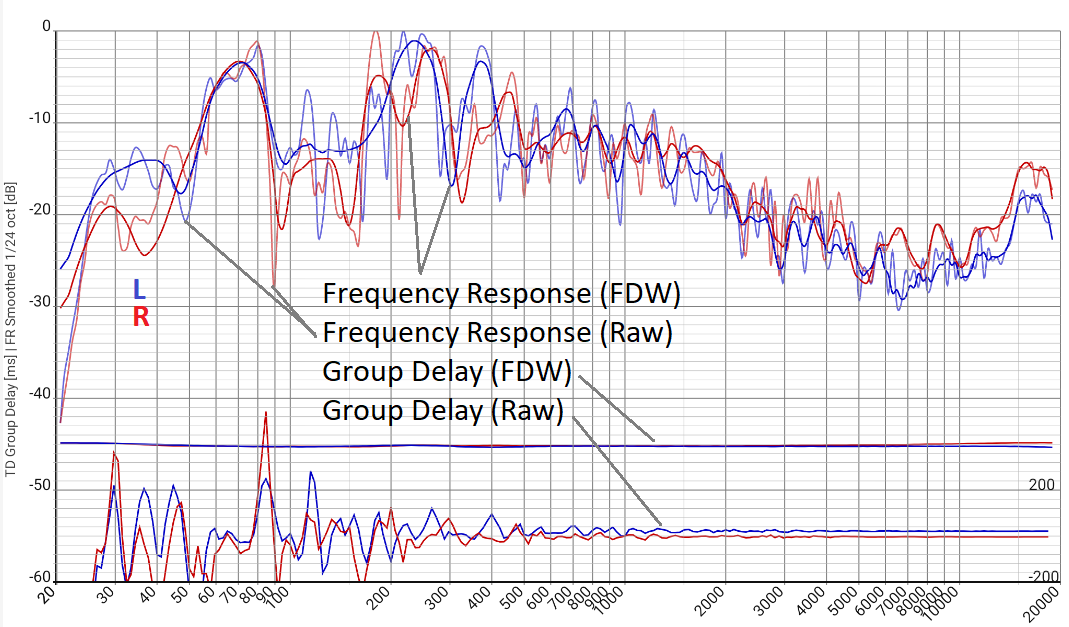

The strong amplitude change is associated with a correspondingly strong phase shift, so that the GLZ "Group Delay (Raw)" literally jumps by more than 500 ms. Admittedly, this is a kind of record value, but changes of over 100 ms with barely 10% frequency change are not uncommon, regardless of listening room, equipment and software. This in itself is of course counterintuitive - surely there is no living room in which two such neighboring tones arrive so differently, as if they had traveled a path difference of approx. 30 m (100 ms), and certainly not over 150 m (500 ms). The "Group Delay (FDW)" curve shows the same measurement data on the same scale, but with frequency-dependent windowing FDW (see later). The value range of perhaps 20 ms is just about recognizable and certainly much more reasonable.

As the author of the app and documentation, I wanted to get to the bottom of the matter to be on the safe side. Some of the results are so interesting that I want to show them here. To investigate, I played back bursts at these frequencies and compared the oscillograms with those of the microphone signals. Because some singularities in waves are related to non-linearities, I used the real physical microphone signal instead of a calculated convolution of these bursts with the impulse response.


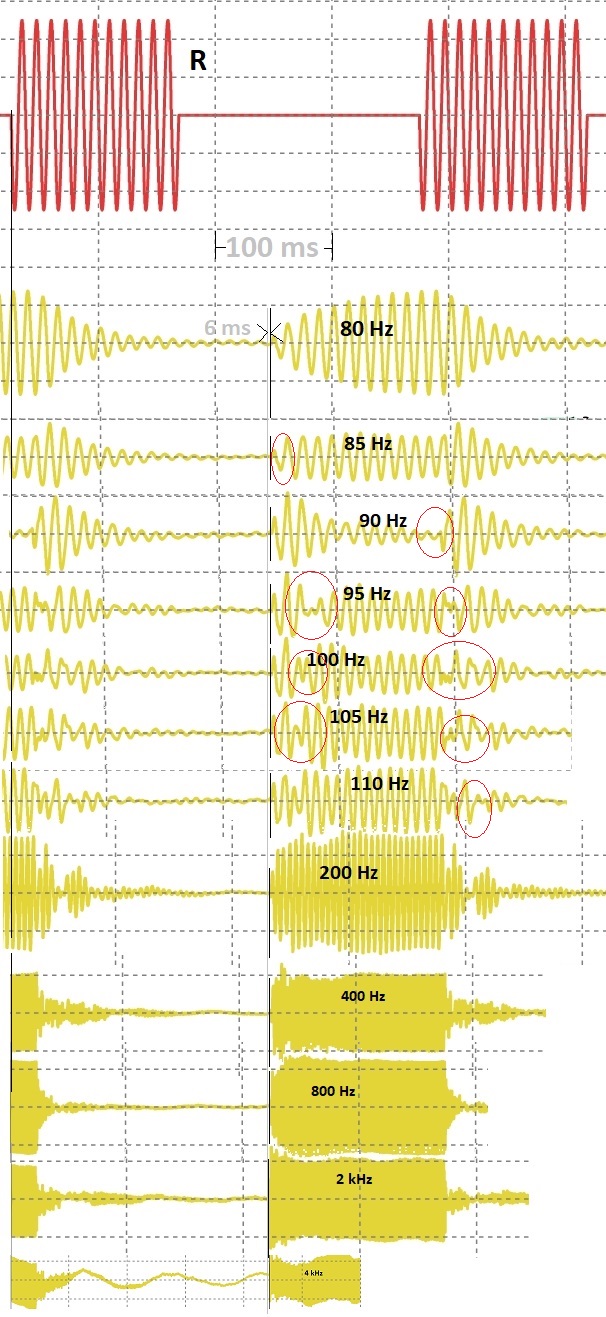
Bursts, played back and recorded with Hifi apps Car Audio Setup. Red: Played burst (only shown for 80 Hz). Yellow: Microphone signals of all frequencies. The beginnings were always aligned at the same distance from the respective signals played back (hence the jumps in the grid) and marked with a thin black line. The vertical gray line 6 ms in ahead is for orientation only.

You can see at first glance that the beginnings of the bursts are shifted by a few ms at most; shifts of the magnitude mentioned above are, as expected, unthinkable. However, the origin of this effect can be seen: The phase jumps at the points circled in red. It is obvious that the cause, similar to the excess phase (see above), is to be found in the additive interaction of the transfer functions of the space. However, the total phase is calculated according to the phase of all (eventually) arriving signal components of the respective frequency. The GD is in turn calculated from the change in this total phase per frequency change. Accordingly, a considerable jump appears in the result. Technically speaking, the frequency of the envelope is so close to the carrier frequency, that the "transit time" of the wave packet is no longer described (see later).

For the sense of hearing, however, this effect plays a completely different role than the first arrival time of the first direct sound (thin black lines): The latter is crucial for a travel-time-based localization of the sound source. And presumably we are the ancestors of those who mastered the time-of-arrival-based localization of a roaring tiger independently of any reflections and phase rotations. This can and should be taken into account in the calculation by using (if not the black line, then at least) only the first wave trains of the measurement are considered. This, in turn, is the main idea behind FDW.

However, you can also see that the measurement result without FDW is not worthless. The peak indicates a clear characteristic in the acoustics, albeit through possibly enriching indirect sound. You could now play sounds at this frequency, walk around the room and check whether this particular feature was already perceived as disturbing in the past and, if necessary, improve the situation. A quantitatively meaningful result is only obtained after FDW. This is also used, for example, as the basis for digital room correction. The common opinion [Barnett 2017] is that digital room correction (DRC) must be based on measurements with FDW. However, the smoothed version without FDW is perfectly adequate for simple adjustment work such as the delay of a subwoofer.

Details and possible points of criticism

Criticism: The evaluation was carried out graphically using the measured oscillograms, and the start times were drawn subjectively at the first visible oscillation. In the calculation below, for example, the GD is not this beginning, but the point of the half rise.
My answer: This may be common in signal theory, but it does not take into account the logarithmic perception of the sense of hearing and the importance of the first direct sound. The thesis "perception begins as soon as you see something on the oscillogram" is certainly not perfect, but it is closer to reality. In addition, the values would practically only change significantly up to the 85 Hz measurement, and almost not at all at the neighboring points up to 110 Hz.

Criticism: The measurement should be replaced by the mathematically correct variant "Convolution of the impulse response with the bursts".
My answer: I have done this and there are no visible differences. The calculation of the somewhat strange-looking 90 Hz oscillogram compared to the measurement above:

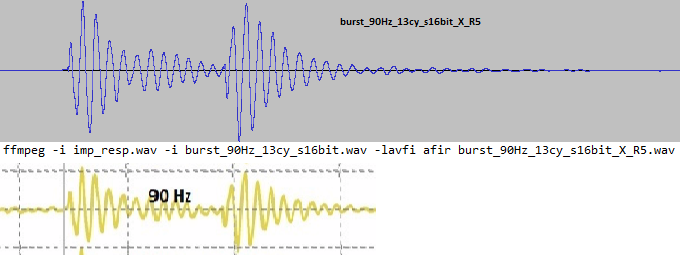
The effects therefore also occur in linear, time-invariant systems and the cause is not to be found in non-linearities. Even more measuring points would not provide any new insights. Basically, two points would be enough to show the discrepancy in the values.

Criticism: The bursts are not windowed, so the measurement is correspondingly inaccurate.
My answer: Certainly much more accurate than the 500 ms found. The room and loudspeaker provide a certain windowing anyway and the wave trains with the frequencies to be examined are clearly visible in the oscillograms, The influence of the harmonics of the circumscribing rectangle can therefore not be too strong.

Detail: FDW settings for the relevant frequency range: 34-59 Hz: 132 ms Window width (je 25 ms rise / fall), 59-103 Hz: 96 ms (21 ms), 103-179 Hz: 72 ms (18 ms), i.e. at the lower limit of what is usual (very short windows).

Question: What accuracy can be expected from a GD measurement?
My answer: With reasonably selected FDW parameters, hopefully in the range of the perception threshold of the sense of hearing, but not much better. Basically, you would have to look at the oscillograms of different frequencies individually (automatically?) and compare them with your knowledge of psychoacoustics. If you calculate a DRC from the measured phase, you should simply carry out various evaluations and look for the best result using a listening test.

Phase

You can rotate the phase of a subwoofer by 180° by reversing the polarity of the speaker. Especially with subwoofers placed on the side opposite to the speakers, this can improve the sound. Some sound processors also offer finer phase settings between 0 and 180°, which can further improve the sound.

Videos (German)


Use in YouTube ⚙ Subtitles for videos in German language.

Part 1 of 4: What is the phase control on the subwoofer for, what does delay mean? How can you adjust it with a centimeter ruler and smartphone?

Part 2 of 4: What exactly does the Speaker Management Unit Behringer Ultra Drive DCX 2496 do when you adjust phase and delay? Function generator and oscilloscope show details that cannot be seen with soundcard and software. By the way, an interesting peculiarity of the 2 kW Class D amplifier STA 2000D from IMG Stageline is found by chance.

Part 3 of 4: What do software products like REW or Acourate measure and show?

Part 4 of 4: : Interpretation of the results

Opportunities for improvement

In addition to the improvement possibilities described above, Hifi-Apps give further hints based on the impulse responses of the individual loudspeakers at the individual listening positions. The topic is constantly being developed, so only some general statements are made here: In particular, clear weaknesses in channel uniformity and also reverberation times that indicate very little damping can significantly degrade the sound. Both can be easily measured with Hifi-Apps and often just as easily corrected. Before any measurement, the general notes on speaker placement and subwoofer placement should be considered.

For technicians

By Fourier transforming the transfer function of a linear time-invariant system, a time shift (delay) $\tau_{d}$ becomes a frequency-proportional phase shift: $ \mathscr{F}\{ F(\omega)\} = f(t) \Rightarrow \mathscr{F}\{\exp(i \omega \tau_{d}) F(\omega)\} =f(t-\tau_{d})$ where $\omega$ is the angular frequency and $t$ is the time. In other words, in this simple case the transfer function can be taken as $H(\omega)=k\exp(i \omega \tau_{d}) $, i.e. $$ \begin{align} |H( \omega)| &= k \\ \angle H( \omega) &: = \varphi = -\omega \; \tau_{d}\\ \end{align} $$ Because of the linear relationship between $\omega$ and $\angle H(\omega)$, the delay can consequently be written both as a fraction and as a differential quotient: $$ \tau_{d} = - \frac{ \varphi( \omega)}{\omega} = - \frac{ \mathrm{d}\varphi( \omega)}{\mathrm{d}\omega} $$

Alternatively, one can assume a frequency dependent behavior of the transfer function. If one neglects the amount$\frac{\mathrm{d}}{\mathrm{d\omega}} |H(\omega)| = 0$, which is unimportant for the time behavior, then $\tau_{d}=-\varphi'$ describes the first element of the Taylor evolution of $H$ around $\omega_0$: $$ \begin{align} Y_k(\omega) &= H_k(\omega) X_k(\omega) \\ &= |H(\omega_0)| \exp\Big(i \varphi(\omega_0) + i (\omega-\omega_0) \varphi'(\omega_0) \Big) X_k(\omega) \\ &= \Bigg( |H(\omega_0)| \exp\Big(i \varphi(\omega_0) -i \omega_0 \varphi'(\omega_0) \Big) \Bigg) \exp\Big(i \varphi'(\omega_0)\omega\Big) X_k(\omega) \end{align} $$ The first bracket has a constant value, the second bracket characterizes the phase rotation by the delay.
Descriptively, both equations state that if one wave train of a certain frequency is needed to bridge a certain distance, WLOG two wave trains of twice the frequency are needed. In the real world, of course, this simple relationship is lost. But it remains useful to split the phase rotation into a trivial part $\tau_{pd}$ describing the time shift and the (mostly crucial) part determining the frequency dependence of the system due to resonances, filter effects etc. $$ \begin{align} \tau_{pd} &= -\frac{\mathrm{d} \varphi(\omega)}{\mathrm{d}\omega} \bigg \vert_{\omega = \omega_0} \\ \tau_{gr} &= -\frac{\mathrm{d} \varphi(\omega)}{\mathrm{d}\omega} \\ \end{align} $$ Software for displaying the group delay therefore offers an "unroll function", which automatically or manually allows the subtraction of a $\tau_{pd}$ portion. This gives the user the possibility to view the system behavior determined by resonances, filter effects etc. without disturbing phase rotations. In practice, this component plays in much slower time scales than the period of the signal, it rather changes the envelope. As shown above, this must be ensured by appropriate windowing when measuring room acoustics, otherwise $\tau_{gr}$ does not reflect the common definition "...how long it takes for a certain frequency to be reproduced...". If one sets a signal with a carrier frequency $\omega$ modulated by an envelope, then $\tau_{gr}$ and $\tau_{pd}$ split accordingly in the transmission: $$ x(t) = \underbrace{ m(t)}_{\text{ Enveloping curve }} \underbrace{ \cos(\omega t)}_{\text{ Carrier freq }} \longrightarrow \underbrace{ m(t-\tau_{gr} )}_{\text{ Enveloping curve }} \; \underbrace{ \cos(\omega (t- \tau_{pd} ))}_{\text{ Carrier freq }} $$ A pure phase delay $\tau_{pd}$ can be accommodated in the cos term as described above, the crucial remainder shifts the envelope depending on which frequency it envelopes. The frequency-dependent change in amplitude was omitted for simplicity.

In discrete-time transmission systems, as represented by digital signal processing, the discrete group delay is related to the sampling interval $T$: $$ \frac{\tau_d(\Omega)}{T} = - \frac{\mathrm{d}\,\operatorname{arg}\{H(e^{i\Omega})\} }{\mathrm{d}\Omega} $$ with the angular frequency $\Omega$ normalized to the sampling frequency $f_s$: $$ \Omega = \frac{\omega}{f_\mathrm{s}} = \omega \cdot T $$ The advantage of the normalized form in discrete-time systems is the independence from concrete sampling frequencies.

Example

Let the transfer function of a discrete system be an averaging over the first 5 indices, i.e. $$ \begin{align} h[n] &= \frac{1}{5} (\delta(n) + \delta(n-1) + \delta(n-2) + \delta(n-3) + \delta(n-4)) \\ H(\Omega) &= \frac{1}{5} (e^{-i0} + e^{-i\Omega} + e^{-i2\Omega} + e^{-i3\Omega} + e^{-i4\Omega} ) \\ &= \frac{1}{5} ( e^{i2\Omega} + e^{i\Omega} + e^{0} + e^{-i\Omega} + e^{-i2\Omega} ) e^{-i2\Omega} \\ &= \frac{1}{5} ( 2 \cos(2 \Omega) + 2 \cos( \Omega) +1) e^{-i2\Omega} \\ \end{align} $$ The cos terms in the brackets (the amplitude response) are real, only the last multiplicand has influence on the phase. Consequently the group delay becomes $$ \tau_{\rm gr}(\Omega) = - \frac{\mathrm{d}\varphi(\Omega)}{\mathrm{d}\Omega} = - \frac{\mathrm{d} (-2\Omega)}{\mathrm{d}\Omega} = 2 $$ This can be understood if you imagine a step function as a signal, which jumps at $t=t_0=0$ from 0 to 1. When the signal reaches the system, at $t<0$ the output becomes 0, then at $t=0, 1, 2, 3, 4$ to $1/5$, $2/5$, $3/5$, $4/5$, $1$, i.e. after the group delay time the mean of the flank is reached.

By the way, the example is a linear phase filter: the phase includes only the $\arg \exp(-i2\Omega)$ term. Roughly speaking, this ultimately comes from the symmetrical structure of the 5 coefficients. While linear-phase filters usually have their maximum in the middle of the impulse response due to this symmetrical structure, the minimum-phase version of the same filter (with the same amplitude response) has the largest coefficients at the beginning of its impulse response. On [falstad.com] different filters can be simulated.

Some measuring devices can calculate (approximate values for) the group delay (directly) from two phase measurements at neighboring frequencies The app "Subwoofer Optimizer" determines the transfer function via logsweep, which is evaluated with Farina's algorithm. The group delay is determined (after smoothing) from the differential quotient of the phase.

References

[Barnett] Mitch Barnett: Accurate Sound Reproduction Using DSP. ‎ Independently published (2 April 2017) ISBN-10 ‏ : ‎ 1520977905 ISBN-13 ‏ : ‎ 978-1520977904

[Blauert 1978] Blauert, J. and Laws, P: "Group Delay Distortions in Electroacoustical Systems" Journal of the Acoustical Society of America Volume 63, Number 5, pp. 1478-1483 (May 1978)

[Burkowitz, Fuchs 2009] Peter K. Burkowitz, Helmut V. Fuchs "Das vernachlässigte Bass-Fundament" Vereinszeitschrift des Verbands Deutscher Tonmeister 2/2009 p. 35

[Goertz 2001] Goertz A, Wolff M (2001) "Neue Methoden zur Anpassung von Studiomonitoren an die Raumakustik mit Hilfe digitaler Filterkonzepte" Teil 1 von 2. Fortschritte der Akustik, DAGA 2002 http://www.ifaa-akustik.de/files/DAGA2002-Teil1.PDF http://www.ifaa-akustik.de/files/DAGA2002-Teil2.PDF

[Goossens] Sebastian Goossens "Wahrnehmbarkeit von Phasenverzerrungen" Institut für Rundfunktechnik, München https://forum2.magnetofon.de/bildupload/goosphase.pdf

[MSO] Multi Subwoofer Optimizer, Andy C https://www.avsforum.com/threads/optimizing-subwoofers-and-integration-with-mains-multi-sub-optimizer.2103074/

[Münker 2016] Christian Münker: "DSP auf FPGAs: Kap. 5-2 Do-It-Yourself FIR Filterentwurf" https://www.youtube.com/watch?v=y0PNXUI5x1U

[falstad.com] "...some educational applets I wrote to help visualize various concepts in math, physics, and engineering..."
http://www.falstad.com/mathphysics.html
http://falstad.com/dfilter/

[Welti Devantier] Todd Welti, Allan Devantier: Low-Frequency Optimization Using Multi Subwoofers. Harman International Industries Inc. Northbridge CA 91329 USA, Manuscript received 2006

[earl Geddes] mehlau.net/audio/multisub_geddes

[Welti Harman] Subwoofers: Optimum Number and Locationsby Todd Welti Research Acoustician, Harman International Industries, Inc.twelti@harman.com multsubs_0.pdf links folien rechts text Seite 4 "Multiple Subwoofers != Multiple Subwoofer Channels"

[Earl Geddes - YoutTube] Earl Geddes on Multiple Subwoofers in Small Rooms https://www.youtube.com/watch?v=SCWL-zusyqw

[MSO Software] https://www.andyc.diy-audio-engineering.org/mso/html/rev_hist.html

Forendiskussion. Aktuell (Okt 2020) 234 Seiten. https://www.diyaudio.com/forums/subwoofers/134568-multiple-subs-geddes-approach-149.html

Eine Art Review mit Raummoden, Welti, Geddes etc. Subwoofer / Low Frequency Optimization By Amir Majidimehr [Note: This article was published in the May/June 2012 issue of Widescreen Review Magazine]